Can You Write Your Own Algorithm? [Data Structures & Algorithms]

I had the same question. I am a newbie to the algorithms, I know the basic concepts but I never really got to use them in my day to day work. So, I thought of learning them slowly, one by one. I just wanted to improve my skills as a developer and what better way to do that besides becoming well-versed with the Datastructures and algorithms?

The first one that I learnt was the Binary Search Algorithm. It is very simple and efficient. I went through the concept and also tried using it in a program for sorting an array. I used Java since I am familiar with it.

I also wanted to measure the performance of the algorithm, not just learn to use it. I wanted to know more, so I started digging deep.

Below is the program that I wrote using the Binary Search algorithm to sort an integer array. I also added start and end time variables to measure the overall run time.

public class stepBinaryTreeSearch {

public static void main(String[] args) {

long startTime = System.currentTimeMillis();
int array[] = new int[250000];
int target = 33;

for (int i = 0; i < array.length; i++) {
array[i] = i;
}

int index = binarySearch(array, target);

if (index == -1) {
System.out.println(target + " not found");
} else {
System.out.println("n Element found at: " + index);
}

long endTime = System.currentTimeMillis();
System.out.println("n Total Time taken : " + (endTime - startTime) + "ms");
}

private static int binarySearch(int[] array, int target) {

int steps = 0;
int low = 0;
int high = array.length - 1;

while (low <= high) {
int middle = low + (high - low) / 2;
int value = array[middle];
steps++;

if (value < target)
low = middle + 1;
else if (value > target)
high = middle - 1;
else {
System.out.println(" Total Steps : " + steps);
return middle; // target found
}

}

System.out.println(" Total Steps : " + steps);
return -1;
}

}

Results:

The console shows the below,

1. The size of the array

2. The number of steps to find the element

3. The total execution time

Target : 33 Input Array : 250000

Total Steps : 18

Element found at: 33

Total Time taken : 2ms

This is really a good technique to search and find an element in a sorted array.

My Version:

Now, I had an idea!

What if we could slightly modify the algorithm logic and make it even faster?

Wouldn’t that mean creating my own version of the algorithm?

I was excited and wanted to try it. So, I started modifying the code. I took the same method and changed it a little bit.

The Binary Search works by identifying a center position and then comparing the value in that position with the search value. Based on the comparison, we will ignore either part of the array. For example, we will ignore the right side of the array (which starts in the center and ends with the very last element) if the input search value is lesser than the center value and ignore the left side if the value is bigger.

My idea is this:

what if I could do one more round of comparison again with the new center position of the part of the array that we just selected?

Wouldn’t this speed up the process and reduce the number of steps needed?

I completed the new logic and started testing it. But, the results are not what I expected. Below is my revised method. For now, I am going to just keep it in an elaborative manner for the sake of understanding. Later, I will be refactoring it to be even more efficient & precise.

// my version
private static int modifiedBinarySearch(int[] array, int target) {

int steps = 1;
int low = 0;
int high = array.length - 1;
int middle = 0;
int currentValue = 0;

while (low <= high) {

int newMiddle = 0;
int newCurrentValue = 0;

middle = low + (high - low) / 2;
currentValue = array[middle];

steps++;

if (currentValue < target) {
low = middle + 1;
newMiddle = low + (high - low) / 2;
newCurrentValue = array[newMiddle];

if (newCurrentValue < target) {
low = newMiddle + 1;
} else if (newCurrentValue > target) {
high = newMiddle - 1;
}
} else if (currentValue > target) {
high = middle - 1;
newMiddle = low + (high - low) / 2;
newCurrentValue = array[newMiddle];

if (newCurrentValue > target) {
high = newMiddle - 1;
} else if (newCurrentValue < target) {
low = newMiddle + 1;
}
} else {
System.out.println(" Total Steps : " + steps);
return middle; // target found
}
}

return -1;
}

New Results:

The console shows the below,

1. The size of the array.

2. The number of steps to find the element.

3. The total execution time.

Target : 33 Input Array : 250000

Total Steps : 11

Element found at: 33

Total Time taken : 2ms

I was able to reduce the number of steps needed from 18 to 11. But the execution time stays the same as 2ms. When I run it multiple times, it behaves either a little less or more with respect to the time taken.

When I increase the array size, it seems to be faster by a very little margin in the runtime. But, when the inputs are considerably smaller, it is either equal or a little slower in the runtime.

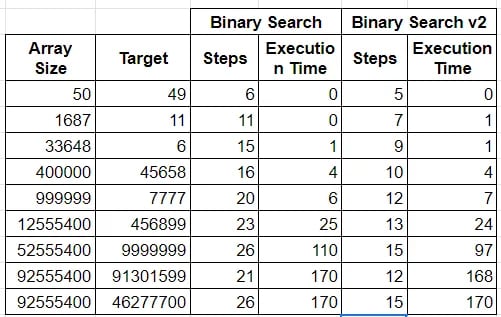
Comparing Various Inputs:

I compared both methods with various inputs and below are the results. It is not definitely what I was expecting.

Summary:

To summarize, I succeeded partially in my attempt today.

• My new revision of the Binary Search Algorithm (I call it the Binary Step Search Algorithm) was able to reduce the number of steps required to find the element in an array.

• Unfortunately, it did not improve the runtime considerably when compared to the original Binary Search Algorithm.

I consider this a partial success since I learn a lot from this experience, and I will not easily forget the Binary Search Algorithm ever.

At this moment, I couldn’t come up with a new algorithm or improve an existing one. However, I am satisfied that I explored my idea. I suppose I could keep continuing to explore my thought process. Who knows? I may stumble upon a remarkable idea someday.